Tuples and Structures
Tuples
Tuples are pretty much what you think they are. They have an ordering and everything. You specify them with <<>> and they are 1-indexed.
Did I mention they’re 1-indexed? They’re 1-indexed.
x == <<4, 5, 6>>;
x[1] + x[2] + x[3] = 15;
In addition, you have the DOMAIN operator. DOMAIN Tuple is the set 1..Len(Tuple). For example, DOMAIN <<"hello", "world", "!">> = {1, 2, 3}.
If you add EXTENDS Sequences to your spec, they also do double duty as sequences, which adds some more functionality. None of these operations will mutate the sequence. If you want to pop the head, for example, you have to do seq := Tail(seq).
| operator | operation | example |
|---|---|---|
| Head | First element | Head(<<1, 2>>) = 1 |
| Tail | Sequence aside from head | Tail(<<1, 2>>) = <<2>> |
| Append | Add element to end of sequence | Append(<<1>>, 2) = <<1, 2>> |
\o |
Combine two sequences | <<1>> \o <<2>> = <<1, 2>> |
| Len | Length of sequence | Len(<<1, 2>>) = 2 |
Note that these use parenthesis, unlike DOMAIN, SUBSET, and UNION. A very rough rule of thumb is that if it’s from a module, it uses parenthesis, and if it’s part of the core language, it will be in ALL CAPS.
If the value is undefined (for example, Tail(<<>>)), the model considers that an error in your spec. And let’s be honest, it probably is.
Write an operator that takes a tuple and, if the tuple is length two, returns the reversed tuple, and otherwise returns the original tuple.
Reverse(Twople) == IF Len(Twople) = 2 THEN <<Twople[2], Twople[1]>> ELSE Twople
Sets of Tuples
Sometimes, you need a set of tuples or sequences. For example, given a chessboard, you might represent the squares as a pair of two integers. The construct, then, for every possible point in the grid would be (1..8) \X (1..8). \X here is the Cartesian product operator: set1 \X set2 is the set of all tuples t where t[1] \in set1 and t[2] \in set2.
chessboard_squares == {"a", "b", "c", "d", "e", "f", "g", "h"} \X (1..8)
<<"a", 2>> \in chessboard_squares
<<"b", 10>> \notin chessboard_squares
You can combine more than two sets with \X, but how they combine depends on how you group the sets. Given a \in A, b \in B, and c \in C:
<<a, b, c>> \in A \X B \X C
<<<<a, b>>, c>> \in (A \X B) \X C
<<a, <<b, c>>>> \in A \X (B \X C)
The first is a tuple of length three, the latter two are tuples of length two, one element of which is a tuple of length two.
Structures
Structures are hashes. They have keys and values. You specify them as [key |-> value] and query them with either ["key"] or .key. Both are legal and valid.
x == [a |-> 1, b |-> {2, 3}];
x.a = 1;
x["b"] = {2, 3};
Aside from that, there’s one extra trick structures have. Instead of key |-> value, you can do key : set. In that case, instead of a structure you get the set of all structures which have, for each given key, a value in the set.
x == [a : {1}, b : {2, 3}];
x = { [a |-> 1, b |-> 2], [a |-> 1, b |-> 3] }
You can also use DOMAIN on structures, which will give the set of keys, as strings.
If you use : syntax and any of the values are not sets, then the entire construct is invalid. In other words, while [a: {1}, b: {2,3}] is the above set, [a: 1, b: {2, 3}] will throw an error if you try to use it.
Type Composition
Any type can be squeezed inside any other type.
x == [a |-> {<<>>, <<1, 2, 3>>, <<3, 2, 1>>}, b |-> <<[a |-> 0]>>];
x.b[1].a; \* 0
There’s nothing technically stopping you from writing a sequence with alternating 1’s and sets of structures, but that will end very badly, so please don’t do that.
Example
Solve the Tower of Hanoi.
This kind of problem flips TLA+ on its head. Instead of checking if our solution has no problems, we’re checking that our problem has a solution! A common way to do this is to turn the spec inside out: we say the spec is “valid” if the solution is unreachable. Then TLC will flag it as an “error” and show us the steps required to reproduce the solution.
---- MODULE hanoi ----
EXTENDS TLC, Sequences, Integers
(* --algorithm hanoi
variables tower = <<<<1, 2, 3>>, <<>>, <<>>>>,
define
D == DOMAIN tower
end define;
begin
while TRUE do
assert tower[3] /= <<1, 2, 3>>;
with from \in {x \in D : tower[x] /= <<>>},
to \in {
y \in D :
\/ tower[y] = <<>>
\/ Head(tower[from]) < Head(tower[y])
}
do
tower[from] := Tail(tower[from]) ||
tower[to] := <<Head(tower[from])>> \o tower[to];
end with;
end while;
end algorithm; *)
====
Everything should look familiar with the exception of the set syntax we use to define “from” and “to”. We’re covering that in more detail next section, but for now, it’s roughly a set filter. For example, from is defined as being one of the numbers such that that tower has at least one element in it.
For to, we pull it from a more restricted set: We either want the tower to be empty, or have a bigger top stone than the tower we’re moving from. Finally, in the block itself, we simulate a move with Tail and concatting. The concat is a bit of a hack, actually- while it seems like Append would be the appropriate operator here, it would put it at the wrong end of the sequence. For example, Append(<<2, 1>>, 3) = <<2, 1, 3>>, when we actually want <<3, 2, 1>>.
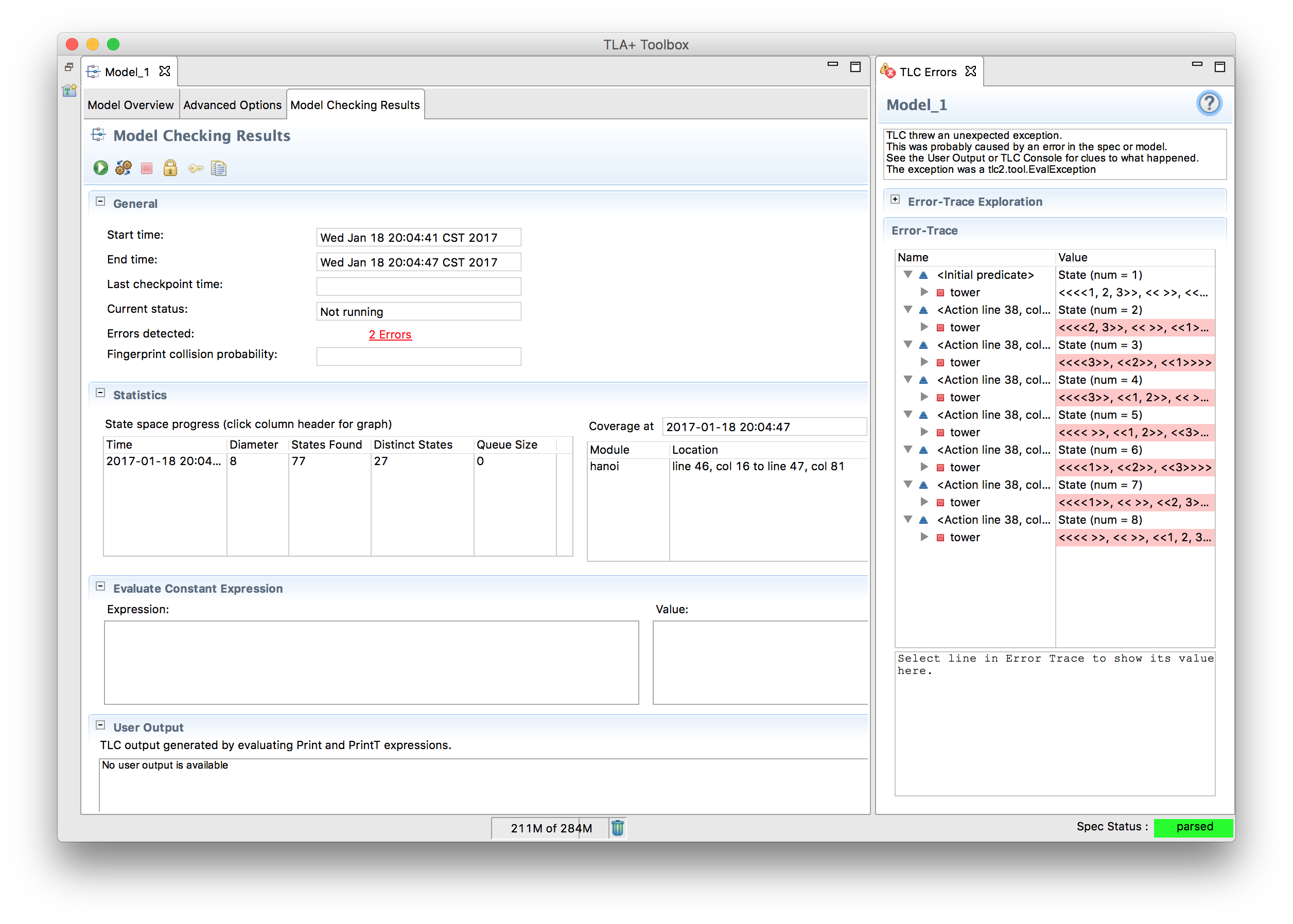
Running this model throws an ‘error’ and shows the steps required to reproduce the bug, aka find the solution. In general, TLA+ isn’t that well suited for solving constraint problems like these, but it can be used to do so in a pinch. Another common example is using TLA+ to solve the water bucket puzzle.